Dalam kehidupan sehari-hari, kita sering menemukan benda-benda berbentuk lingkaran, seperti roda kendaraan, uang logam, piring, atau bahkan lingkaran di lapangan olahraga. Pemahaman tentang rumus keliling lingkaran sangat penting karena dapat digunakan dalam berbagai situasi, mulai dari perhitungan jarak tempuh roda hingga pengukuran luas area yang melibatkan bentuk lingkaran. Artikel ini akan membahas secara lengkap mengenai rumus keliling lingkaran, contoh soal, dan pembahasannya.
Keliling lingkaran adalah jumlah keseluruhan garis yang mengelilingi bidang tersebut. Dalam matematika, keliling lingkaran dapat dihitung dengan menggunakan dua rumus utama, yaitu rumus yang menggunakan diameter dan rumus yang menggunakan jari-jari. Kedua rumus ini sangat berguna dalam berbagai perhitungan geometri, terutama ketika kita diberikan informasi tentang ukuran diameter atau jari-jari suatu lingkaran.
Untuk mempermudah pemahaman, artikel ini akan menjelaskan bagaimana menerapkan rumus tersebut dalam berbagai kasus nyata. Dengan contoh soal yang disertai penjelasan langkah demi langkah, pembaca akan lebih mudah memahami konsep dasar serta aplikasi praktis dari rumus keliling lingkaran. Selain itu, artikel ini juga akan memberikan panduan tentang kapan sebaiknya menggunakan nilai π (pi) sebagai 22/7 atau 3,14 agar hasil perhitungan akurat.
Rumus Keliling Lingkaran
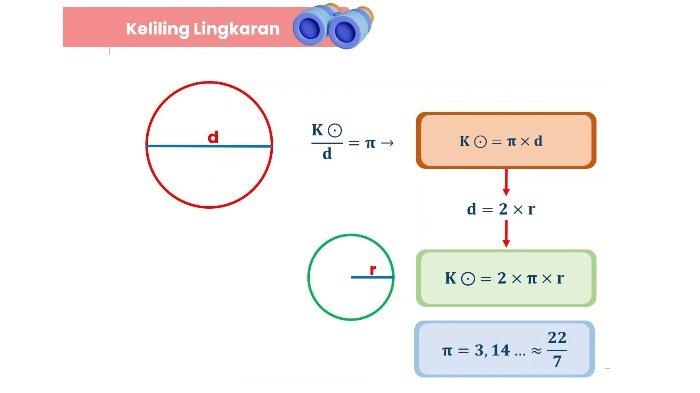
Rumus keliling lingkaran merupakan salah satu konsep dasar dalam geometri. Terdapat dua versi rumus yang umum digunakan, yaitu:
- Menggunakan Diameter
Jika diameter lingkaran diketahui, maka keliling dapat dihitung dengan rumus:
$$
K = \pi \times d
$$
Di mana: - $ K $ adalah keliling lingkaran.
- $ \pi $ (pi) adalah konstanta yang nilainya sekitar 22/7 atau 3,14.
-
$ d $ adalah diameter lingkaran, yaitu dua kali panjang jari-jari ($ d = 2r $).
-
Menggunakan Jari-Jari
Jika jari-jari lingkaran diketahui, maka keliling dapat dihitung dengan rumus:
$$
K = 2 \times \pi \times r
$$
Di mana: - $ K $ adalah keliling lingkaran.
- $ \pi $ (pi) adalah konstanta yang nilainya sekitar 22/7 atau 3,14.
- $ r $ adalah jari-jari lingkaran.
Pemilihan nilai π (pi) bergantung pada kondisi soal. Jika jari-jari atau diameter dapat dibagi 7, gunakan nilai 22/7. Jika tidak, gunakan nilai 3,14 untuk mendapatkan hasil yang lebih akurat.
Contoh Soal dan Pembahasan
Berikut beberapa contoh soal beserta pembahasan yang dapat membantu memahami cara menghitung keliling lingkaran:
Contoh 1: Menghitung Keliling Lingkaran dengan Jari-Jari
Soal: Diketahui jari-jari lingkaran 49 cm. Hitunglah keliling lingkaran tersebut!
Pembahasan:
$$
K = 2 \times \frac{22}{7} \times 49 = 308 \text{ cm}
$$
Contoh 2: Menghitung Keliling Lingkaran dengan Diameter
Soal: Diketahui diameter lingkaran 25 cm. Hitunglah keliling lingkaran tersebut!
Pembahasan:
$$
K = 3,14 \times 25 = 78,5 \text{ cm}
$$
Contoh 3: Menghitung Diameter dari Keliling
Soal: Diketahui keliling lingkaran 28,26 cm. Berapa diameter lingkaran tersebut?
Pembahasan:
$$
28,26 = 3,14 \times d \Rightarrow d = \frac{28,26}{3,14} = 9 \text{ cm}
$$
Contoh 4: Menghitung Jari-Jari dari Keliling
Soal: Sebuah uang logam berbentuk lingkaran memiliki keliling 352 cm. Berapakah jari-jari uang logam tersebut?
Pembahasan:
$$
352 = 2 \times \frac{22}{7} \times r \Rightarrow r = \frac{352 \times 7}{44} = 56 \text{ cm}
$$
Aplikasi Praktis Rumus Keliling Lingkaran
Rumus keliling lingkaran tidak hanya digunakan dalam soal-soal matematika, tetapi juga memiliki banyak aplikasi dalam kehidupan nyata. Misalnya, dalam perencanaan taman, pengukuran jarak tempuh roda mobil, atau penghitungan jumlah pohon yang ditanam di sekeliling taman.
Sebagai contoh, jika sebuah kolam renang berbentuk lingkaran dengan jari-jari 9,5 meter dan ada jalan setapak selebar 0,5 meter di sekelilingnya, maka total diameter lingkaran yang harus dikelilingi adalah 20 meter. Dengan demikian, keliling lingkaran tersebut adalah $ 3,14 \times 20 = 62,8 $ meter. Jika seseorang berlari mengelilingi kolam tersebut sebanyak 10 kali, maka jarak yang ditempuh adalah $ 62,8 \times 10 = 628 $ meter.
Tips dan Trik dalam Menghitung Keliling Lingkaran
-
Pilih Nilai π yang Tepat
Pastikan untuk menggunakan nilai π sesuai dengan kondisi soal. Jika jari-jari atau diameter dapat dibagi 7, gunakan 22/7. Jika tidak, gunakan 3,14. -
Perhatikan Satuan
Pastikan satuan jari-jari atau diameter sesuai dengan satuan yang diminta dalam soal. Misalnya, jika jari-jari diberikan dalam sentimeter, pastikan jawaban juga dalam sentimeter. -
Gunakan Langkah-langkah yang Sistematis
Mulailah dengan menulis rumus yang sesuai, kemudian substitusi nilai yang diketahui, lalu hitung hasilnya secara bertahap.
Penutup
Dengan memahami rumus keliling lingkaran dan menerapkannya dalam berbagai situasi, kita dapat lebih mudah menyelesaikan masalah geometri yang melibatkan lingkaran. Artikel ini telah memberikan penjelasan lengkap, contoh soal, dan pembahasan yang dapat membantu siswa maupun pembaca umum dalam memperdalam pemahaman mereka tentang konsep ini. Semoga artikel ini bermanfaat dan memberikan wawasan yang bermanfaat bagi pembaca.