Rumus sinus, cosinus, dan tangen adalah dasar penting dalam memahami konsep trigonometri. Bagi pelajar matematika, menguasai ketiga rumus ini sangat diperlukan karena sering digunakan dalam berbagai perhitungan dan soal-soal yang berkaitan dengan segitiga siku-siku. Dengan memahami rumus-rumus ini, siswa dapat menyelesaikan masalah geometri secara lebih efisien dan akurat. Selain itu, penerapan trigonometri juga sangat luas, mulai dari teknik sipil hingga ilmu fisika dan astronomi. Oleh karena itu, pemahaman mendalam tentang rumus sinus, cosinus, dan tangen menjadi kunci keberhasilan dalam belajar matematika.
Rumus sinus, cosinus, dan tangen berasal dari hubungan antara sudut dan sisi dalam segitiga siku-siku. Ketiga fungsi trigonometri ini membantu menghubungkan besar sudut dengan panjang sisi segitiga. Misalnya, sinus suatu sudut adalah rasio antara sisi depan sudut terhadap sisi miring, cosinus adalah rasio antara sisi samping sudut terhadap sisi miring, sedangkan tangen adalah rasio antara sisi depan dan sisi samping. Dengan menggunakan rumus-rumus ini, siswa dapat menghitung nilai sudut atau panjang sisi yang tidak diketahui. Pemahaman yang baik akan memudahkan mereka dalam mengerjakan berbagai jenis soal, termasuk yang melibatkan bidang datar maupun ruang.
Selain itu, penggunaan rumus sinus, cosinus, dan tangen juga sangat relevan dalam kehidupan sehari-hari. Contohnya, dalam teknik sipil, para insinyur menggunakan trigonometri untuk menghitung tinggi bangunan atau sudut kemiringan jalan. Di bidang navigasi, rumus-rumus ini digunakan untuk menentukan posisi kapal atau pesawat terbang. Dalam dunia olahraga, atlet sepak bola bisa menggunakan trigonometri untuk menghitung jarak tembakan atau arah passing. Dengan demikian, pemahaman tentang rumus sinus, cosinus, dan tangen bukan hanya penting dalam ujian, tetapi juga dalam berbagai situasi nyata.
Pengertian Dasar Trigonometri
Trigonometri adalah cabang matematika yang mempelajari hubungan antara sudut dan sisi dalam segitiga. Konsep ini sangat berguna dalam menyelesaikan berbagai masalah yang melibatkan ukuran dan bentuk. Trigonometri memiliki tiga fungsi utama, yaitu sinus (sin), cosinus (cos), dan tangen (tan). Ketiga fungsi ini digunakan untuk menghitung rasio antara sisi-sisi segitiga siku-siku terhadap sudut tertentu. Misalnya, jika kita mengetahui besar sudut dan panjang satu sisi segitiga, maka kita dapat menghitung panjang sisi lainnya dengan menggunakan fungsi trigonometri.
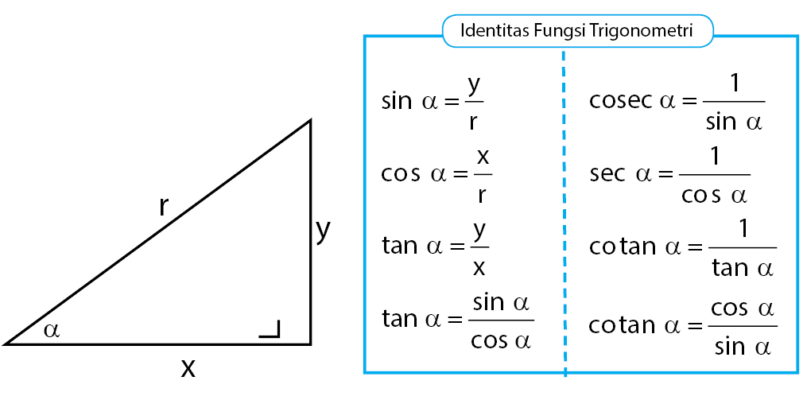
Dalam segitiga siku-siku, terdapat tiga sisi utama, yaitu sisi depan (sisi yang berlawanan dengan sudut yang diberikan), sisi samping (sisi yang berdekatan dengan sudut yang diberikan), dan sisi miring (sisi yang terletak di depan sudut siku-siku). Fungsi sinus didefinisikan sebagai rasio antara sisi depan dan sisi miring, cosinus sebagai rasio antara sisi samping dan sisi miring, serta tangen sebagai rasio antara sisi depan dan sisi samping. Dengan memahami definisi ini, siswa dapat mengaplikasikan rumus-rumus tersebut dalam berbagai situasi.
Penggunaan trigonometri juga tidak terbatas pada segitiga siku-siku. Dalam beberapa kasus, trigonometri digunakan untuk menyelesaikan masalah yang melibatkan lingkaran, gelombang, dan bahkan sistem koordinat polar. Namun, untuk siswa tingkat dasar, fokus utamanya adalah pada segitiga siku-siku. Dengan memahami dasar-dasar trigonometri, siswa dapat memperluas pengetahuan mereka dan menghadapi berbagai tantangan matematika yang lebih kompleks.
Rumus Sinus, Cosinus, dan Tangen
Rumus sinus, cosinus, dan tangen adalah dasar dari trigonometri yang digunakan untuk menghitung hubungan antara sudut dan sisi dalam segitiga siku-siku. Untuk memahami rumus ini, pertama-tama kita harus mengetahui istilah-istilah dasar seperti sisi depan, sisi samping, dan sisi miring. Sisi depan adalah sisi yang berada di hadapan sudut yang diberikan, sisi samping adalah sisi yang berdekatan dengan sudut tersebut, dan sisi miring adalah sisi yang terletak di depan sudut siku-siku.
Rumus sinus dinyatakan sebagai sin θ = sisi depan / sisi miring. Dengan menggunakan rumus ini, kita dapat menghitung besar sudut atau panjang sisi jika dua dari tiga variabel diketahui. Misalnya, jika kita mengetahui panjang sisi depan dan sisi miring, maka kita dapat menghitung besar sudut θ. Sebaliknya, jika kita mengetahui besar sudut dan salah satu sisi, kita dapat mencari sisi lainnya.
Rumus cosinus dinyatakan sebagai cos θ = sisi samping / sisi miring. Mirip dengan rumus sinus, rumus ini juga digunakan untuk menghitung hubungan antara sudut dan sisi dalam segitiga siku-siku. Dengan menggunakan rumus ini, kita dapat menentukan panjang sisi samping jika besar sudut dan sisi miring diketahui.
Sementara itu, rumus tangen dinyatakan sebagai tan θ = sisi depan / sisi samping. Rumus ini sangat berguna dalam situasi di mana kita ingin mengetahui hubungan antara dua sisi segitiga siku-siku tanpa memperhatikan sisi miring. Dengan menggunakan rumus tangen, kita dapat menghitung besar sudut atau panjang sisi jika dua dari tiga variabel diketahui.
Cara Menggunakan Rumus Sinus, Cosinus, dan Tangen
Menggunakan rumus sinus, cosinus, dan tangen memerlukan pemahaman dasar tentang segitiga siku-siku dan bagaimana mengidentifikasi sisi-sisi yang relevan. Pertama-tama, kita perlu menentukan sudut yang ingin kita hitung atau sisi yang ingin kita cari. Setelah itu, kita dapat mengidentifikasi sisi depan, sisi samping, dan sisi miring berdasarkan posisi sudut tersebut.
Misalnya, jika kita ingin menghitung besar sudut θ, kita perlu mengetahui panjang sisi depan dan sisi miring untuk menggunakan rumus sinus, atau panjang sisi samping dan sisi miring untuk menggunakan rumus cosinus. Jika kita ingin menghitung panjang sisi depan, kita dapat menggunakan rumus sinus jika kita mengetahui besar sudut dan panjang sisi miring.
Selain itu, kita juga dapat menggunakan rumus invers untuk menghitung besar sudut jika kita mengetahui rasio antara dua sisi. Misalnya, jika kita mengetahui rasio antara sisi depan dan sisi miring, kita dapat menggunakan fungsi arcsin untuk menghitung besar sudut. Demikian pula, jika kita mengetahui rasio antara sisi samping dan sisi miring, kita dapat menggunakan fungsi arccos, dan jika kita mengetahui rasio antara sisi depan dan sisi samping, kita dapat menggunakan fungsi arctan.
Contoh Soal dan Penyelesaian
Untuk memperjelas penggunaan rumus sinus, cosinus, dan tangen, mari kita lihat beberapa contoh soal beserta penyelesaiannya.
Contoh 1:
Sebuah segitiga siku-siku memiliki sudut θ dengan sisi depan 3 cm dan sisi miring 5 cm. Hitunglah besar sudut θ.
Penyelesaian:
Kita dapat menggunakan rumus sinus:
sin θ = sisi depan / sisi miring
sin θ = 3 / 5
θ = arcsin(3/5)
θ ≈ 36,87°
Contoh 2:
Sebuah segitiga siku-siku memiliki sudut θ dengan sisi samping 4 cm dan sisi miring 5 cm. Hitunglah besar sudut θ.
Penyelesaian:
Kita dapat menggunakan rumus cosinus:
cos θ = sisi samping / sisi miring
cos θ = 4 / 5
θ = arccos(4/5)
θ ≈ 36,87°
Contoh 3:
Sebuah segitiga siku-siku memiliki sudut θ dengan sisi depan 3 cm dan sisi samping 4 cm. Hitunglah besar sudut θ.
Penyelesaian:
Kita dapat menggunakan rumus tangen:
tan θ = sisi depan / sisi samping
tan θ = 3 / 4
θ = arctan(3/4)
θ ≈ 36,87°
Dengan contoh-contoh di atas, kita dapat melihat bagaimana rumus sinus, cosinus, dan tangen digunakan untuk menghitung besar sudut dalam segitiga siku-siku. Pemahaman yang baik tentang rumus-rumus ini akan sangat membantu siswa dalam menyelesaikan berbagai jenis soal trigonometri.
Keuntungan Memahami Rumus Sinus, Cosinus, dan Tangen
Memahami rumus sinus, cosinus, dan tangen memberikan banyak manfaat bagi pelajar matematika. Pertama-tama, pemahaman ini memungkinkan siswa untuk menyelesaikan berbagai masalah geometri dengan lebih cepat dan akurat. Dengan menggunakan rumus-rumus ini, siswa dapat menghitung sudut atau panjang sisi yang tidak diketahui tanpa perlu menggambar segitiga secara manual.
Selain itu, pemahaman tentang trigonometri juga meningkatkan kemampuan analitis siswa. Ketika siswa memahami hubungan antara sudut dan sisi dalam segitiga siku-siku, mereka akan lebih mudah mengenali pola dan struktur dalam soal-soal matematika. Hal ini sangat berguna dalam menyelesaikan soal-soal yang lebih kompleks, seperti yang melibatkan segitiga non-siku-siku atau aplikasi trigonometri dalam bidang lain.
Selain itu, pemahaman tentang trigonometri juga meningkatkan daya ingat dan kemampuan logika siswa. Ketika siswa terbiasa menggunakan rumus sinus, cosinus, dan tangen, mereka akan lebih mahir dalam mengingat dan menerapkan konsep-konsep matematika. Hal ini akan membantu mereka dalam menghadapi ujian atau tugas-tugas matematika yang lebih sulit.
Tips untuk Menguasai Rumus Sinus, Cosinus, dan Tangen
Menguasai rumus sinus, cosinus, dan tangen membutuhkan latihan dan pemahaman yang cukup. Berikut beberapa tips yang dapat membantu siswa dalam menguasai konsep ini.
Pertama, siswa harus memahami dasar-dasar trigonometri, termasuk istilah-istilah seperti sisi depan, sisi samping, dan sisi miring. Tanpa pemahaman ini, siswa akan kesulitan dalam mengidentifikasi sisi-sisi yang relevan dalam segitiga siku-siku.
Kedua, siswa disarankan untuk sering berlatih dengan berbagai jenis soal. Latihan yang rutin akan membantu siswa memahami cara menerapkan rumus sinus, cosinus, dan tangen dalam berbagai situasi. Selain itu, latihan juga akan meningkatkan kecepatan dan akurasi dalam menyelesaikan soal.
Ketiga, siswa dapat menggunakan alat bantu seperti kalkulator atau aplikasi matematika untuk mempermudah perhitungan. Kalkulator dapat digunakan untuk menghitung nilai fungsi trigonometri seperti arcsin, arccos, dan arctan. Aplikasi matematika juga dapat membantu siswa memvisualisasikan segitiga siku-siku dan hubungan antara sudut dan sisi.
Keempat, siswa disarankan untuk mencari referensi tambahan seperti buku teks, video tutorial, atau situs web yang menyediakan penjelasan lengkap tentang trigonometri. Referensi tambahan ini dapat memberikan perspektif yang berbeda dan memperluas pemahaman siswa.
Terakhir, siswa perlu bersabar dan tidak ragu untuk bertanya jika ada hal yang kurang jelas. Trigonometri adalah topik yang cukup rumit, tetapi dengan latihan dan dukungan yang tepat, siswa dapat menguasainya dengan baik.