Matematika sering kali dianggap sebagai pelajaran yang sulit, terutama ketika berkaitan dengan konsep-konsep seperti cosinus, sinus, dan tangen. Namun, sebenarnya jika dipahami dengan benar, rumus-rumus ini bisa menjadi alat kuat untuk menyelesaikan berbagai masalah matematika, baik dalam bidang geometri maupun fisika. Cos Sin Tan adalah bagian dari trigonometri, sebuah cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga. Dengan memahami dasar-dasar cos, sin, dan tan, siswa dapat menguasai topik ini secara lebih mudah dan percaya diri. Artikel ini akan membantu pemula memahami konsep-konsep dasar tersebut, memberikan contoh soal, serta tips praktis untuk meningkatkan kemampuan dalam matematika.
Trigonometri tidak hanya digunakan dalam matematika sekolah, tetapi juga dalam berbagai bidang kehidupan nyata. Contohnya, dalam teknik sipil, arsitektur, atau bahkan dalam pengembangan game komputer. Oleh karena itu, memahami cos, sin, dan tan sangat penting bagi siapa pun yang ingin menguasai matematika. Dengan penguasaan yang cukup, siswa tidak hanya mampu menjawab soal-soal ujian, tetapi juga mampu menerapkan ilmu ini dalam situasi nyata. Artikel ini akan membahas setiap aspek dari cos, sin, dan tan, mulai dari definisi hingga aplikasi praktisnya.
Salah satu tantangan utama dalam belajar cos, sin, dan tan adalah memahami bagaimana cara menghitungnya. Dalam artikel ini, kita akan membahas bagaimana menggunakan kalkulator, tabel trigonometri, atau bahkan menghitung secara manual. Selain itu, kita juga akan melihat bagaimana rumus-rumus ini digunakan dalam menyelesaikan persamaan trigonometri dan masalah geometri. Dengan penjelasan yang jelas dan contoh yang relevan, pembaca akan merasa lebih percaya diri dalam menghadapi soal-soal trigonometri.
Apa Itu Cos Sin Tan?
Cos Sin Tan adalah singkatan dari cosine (cos), sine (sin), dan tangent (tan). Ketiganya merupakan fungsi trigonometri yang digunakan untuk menggambarkan hubungan antara sudut dan sisi-sisi segitiga siku-siku. Dalam segitiga siku-siku, tiga fungsi ini didefinisikan sebagai rasio antara dua sisi segitiga. Misalnya, cosinus suatu sudut adalah rasio antara sisi samping dan sisi miring, sinus adalah rasio antara sisi depan dan sisi miring, sedangkan tangen adalah rasio antara sisi depan dan sisi samping.
Pemahaman tentang fungsi-fungsi ini sangat penting karena mereka sering digunakan dalam berbagai bidang, termasuk sains, teknik, dan teknologi. Dalam fisika, misalnya, cos dan sin digunakan untuk menghitung gaya atau kecepatan dalam arah tertentu. Di bidang navigasi, fungsi-fungsi ini membantu menentukan posisi dan jarak. Dengan demikian, memahami cos, sin, dan tan bukan hanya bermanfaat untuk ujian matematika, tetapi juga untuk penggunaan nyata dalam kehidupan sehari-hari.
Bagaimana Cara Menghitung Cos Sin Tan?
Menghitung nilai cos, sin, dan tan dapat dilakukan dengan beberapa cara, tergantung pada jenis soal yang diberikan. Salah satu metode yang umum digunakan adalah dengan menggunakan kalkulator. Pada kalkulator ilmiah, pengguna dapat memasukkan besar sudut dalam derajat atau radian, lalu mengklik tombol cos, sin, atau tan untuk mendapatkan hasilnya. Namun, bagi pemula, penting untuk memahami prinsip dasar dari fungsi-fungsi ini agar tidak hanya mengandalkan kalkulator.
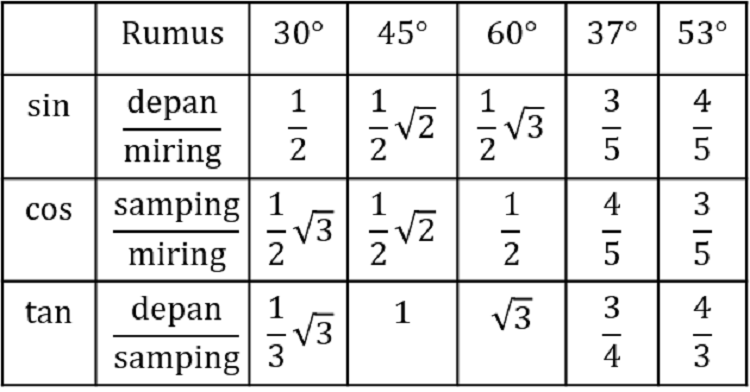
Selain kalkulator, tabel trigonometri juga bisa digunakan untuk mencari nilai-nilai cos, sin, dan tan dari sudut-sudut tertentu. Tabel ini biasanya menyertakan nilai-nilai dasar seperti 0°, 30°, 45°, 60°, dan 90°. Untuk sudut-sudut yang tidak ada dalam tabel, pengguna dapat menggunakan interpolasi atau rumus-rumus trigonometri lanjutan. Dalam kasus tertentu, seperti saat tidak memiliki akses ke kalkulator atau tabel, nilai-nilai ini juga bisa dihitung secara manual dengan menggunakan deret Taylor atau pendekatan lainnya.
Contoh Soal dan Penyelesaian
Untuk memperkuat pemahaman, berikut adalah beberapa contoh soal yang melibatkan cos, sin, dan tan beserta penyelesaiannya. Pertama, mari kita lihat soal yang melibatkan segitiga siku-siku. Misalnya, jika sebuah segitiga memiliki sudut 30° dan sisi miring sepanjang 10 cm, berapa panjang sisi depan? Dalam hal ini, kita dapat menggunakan fungsi sinus, yaitu sin(30°) = sisi depan / sisi miring. Karena sin(30°) = 0,5, maka sisi depan = 0,5 × 10 cm = 5 cm.
Soal kedua melibatkan penggunaan tangen. Jika sebuah segitiga memiliki sudut 45° dan sisi samping sepanjang 7 cm, berapa panjang sisi depan? Karena tan(45°) = 1, maka sisi depan = 1 × 7 cm = 7 cm. Dengan demikian, segitiga tersebut adalah segitiga sama kaki. Contoh soal ketiga adalah mencari besar sudut jika diketahui nilai sinus. Misalnya, jika sin(θ) = 0,5, maka θ = 30° atau 150°, tergantung pada kuadrannya.
Tips untuk Menguasai Cos Sin Tan
Menguasai cos, sin, dan tan membutuhkan latihan yang konsisten. Berikut beberapa tips yang bisa membantu pemula dalam memahami dan menguasai materi ini. Pertama, gunakan kartu flash untuk menghafal nilai-nilai dasar seperti sin(30°), cos(60°), dan tan(45°). Kedua, latih diri dengan mengerjakan banyak soal, baik dari buku teks maupun situs web yang menyediakan latihan online. Ketiga, coba menggambar segitiga siku-siku untuk memvisualisasikan hubungan antara sudut dan sisi-sisinya.
Selain itu, gunakan aplikasi atau situs web yang menyediakan grafik fungsi trigonometri. Grafik ini membantu memahami bagaimana nilai cos, sin, dan tan berubah seiring dengan perubahan sudut. Terakhir, jangan ragu untuk bertanya kepada guru atau teman jika mengalami kesulitan. Diskusi dengan orang lain bisa membuka wawasan baru dan memperdalam pemahaman.
Aplikasi Praktis Cos Sin Tan dalam Kehidupan Nyata
Meskipun cos, sin, dan tan sering digunakan dalam matematika, mereka juga memiliki banyak aplikasi dalam kehidupan nyata. Dalam bidang teknik, misalnya, para insinyur menggunakan trigonometri untuk menghitung gaya, tegangan, dan kekuatan struktur bangunan. Dalam astronomi, fungsi-fungsi ini digunakan untuk menghitung jarak antar bintang atau planet. Di bidang navigasi, cos dan sin membantu menentukan posisi kapal atau pesawat udara berdasarkan sudut dan jarak.
Dalam dunia digital, cos dan sin juga digunakan dalam pengembangan game dan animasi. Contohnya, dalam game 3D, fungsi-fungsi ini digunakan untuk menggerakkan objek dan membuat efek visual yang realistis. Bahkan dalam musik, trigonometri digunakan untuk menghasilkan gelombang suara yang berbeda. Dengan demikian, memahami cos, sin, dan tan bukan hanya bermanfaat untuk ujian, tetapi juga untuk berbagai bidang kehidupan yang nyata.
Kesimpulan
Cos Sin Tan adalah dasar dari trigonometri, sebuah cabang matematika yang sangat penting dalam berbagai bidang kehidupan. Dengan memahami konsep-konsep dasar ini, siswa dapat menyelesaikan berbagai masalah matematika, baik dalam bentuk soal ujian maupun aplikasi nyata. Artikel ini telah membahas definisi, cara menghitung, contoh soal, dan tips untuk menguasai cos, sin, dan tan. Selain itu, kita juga melihat bagaimana fungsi-fungsi ini digunakan dalam kehidupan sehari-hari. Dengan latihan yang konsisten dan pemahaman yang mendalam, siapa pun dapat menguasai cos, sin, dan tan dan merasa percaya diri dalam menghadapi tantangan matematika.