Bangun datar adalah salah satu konsep dasar dalam matematika yang sering diajarkan sejak dini. Dalam pembelajaran geometri, bangun datar menjadi fondasi untuk memahami berbagai bentuk dan sifat ruang dua dimensi. Pemahaman tentang bangun datar sangat penting karena digunakan dalam berbagai bidang seperti arsitektur, desain grafis, dan teknik. Dengan mengetahui jenis-jenisnya serta sifat-sifatnya, kita dapat lebih mudah menghitung luas, keliling, atau bahkan membuat model tiga dimensi dari benda-benda di sekitar kita.
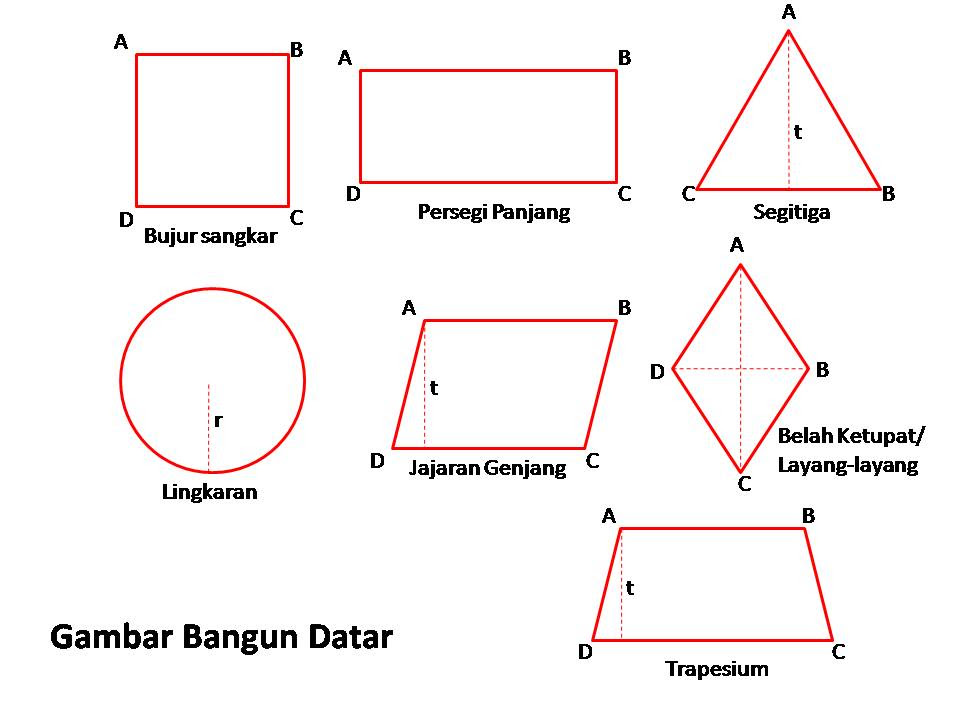
Bangun datar terdiri dari berbagai macam bentuk, mulai dari segitiga, persegi, lingkaran hingga trapesium. Setiap bentuk memiliki ciri khas dan sifat unik yang membedakannya dengan bangun lainnya. Misalnya, segitiga memiliki tiga sisi dan tiga sudut, sedangkan lingkaran memiliki satu sisi yang melengkung sempurna. Pemahaman tentang sifat-sifat ini tidak hanya membantu dalam studi matematika, tetapi juga dalam kehidupan sehari-hari, seperti saat merancang taman, membuat kerajinan tangan, atau bahkan dalam olahraga.
Selain itu, pemahaman akan bangun datar juga bisa meningkatkan kemampuan logika dan analisis. Dengan belajar tentang sifat-sifat setiap bangun, kita bisa menyelesaikan masalah yang berkaitan dengan ukuran, bentuk, dan hubungan antar bangun. Konsep ini juga mendasari banyak teori matematika lanjutan, seperti trigonometri dan kalkulus. Oleh karena itu, mempelajari bangun datar bukan hanya sekadar menghafal rumus, tetapi juga mengembangkan pola pikir yang lebih sistematis dan kritis.
Jenis-Jenis Bangun Datar
Bangun datar dibagi menjadi beberapa jenis berdasarkan jumlah sisi dan bentuknya. Berikut adalah beberapa jenis bangun datar yang umum dikenal:
-
Segitiga
Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Tiga sudut tersebut biasanya berjumlah 180 derajat. Segitiga dapat diklasifikasikan berdasarkan panjang sisinya, seperti segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang. Selain itu, segitiga juga bisa dibedakan berdasarkan besar sudutnya, seperti segitiga siku-siku, segitiga lancip, dan segitiga tumpul. -
Persegi
Persegi adalah bangun datar yang memiliki empat sisi sama panjang dan empat sudut siku-siku. Sifat utama persegi adalah semua sisinya sama panjang dan semua sudutnya 90 derajat. Luas persegi dapat dihitung dengan rumus sisi dikali sisi, sedangkan kelilingnya adalah empat kali panjang sisi. -
Persegi Panjang
Persegi panjang memiliki empat sisi, dua pasang sisi yang sama panjang, dan empat sudut siku-siku. Berbeda dengan persegi, persegi panjang memiliki dua sisi pendek dan dua sisi panjang. Rumus luas persegi panjang adalah panjang dikali lebar, sedangkan kelilingnya adalah dua kali (panjang + lebar). -
Lingkaran
Lingkaran adalah bangun datar yang dibentuk oleh himpunan titik-titik yang memiliki jarak sama dari pusatnya. Jarak tersebut disebut jari-jari. Lingkaran memiliki diameter, yaitu garis lurus yang melewati pusat dan menghubungkan dua titik pada lingkaran. Keliling lingkaran dihitung dengan rumus 2 × π × r, sedangkan luasnya adalah π × r². -
Trapesium
Trapesium adalah bangun datar yang memiliki empat sisi, di mana dua di antaranya sejajar. Sisi yang sejajar disebut sebagai alas dan atas, sedangkan dua sisi lainnya disebut kaki. Trapesium memiliki berbagai jenis, seperti trapesium sama kaki, trapesium siku-siku, dan trapesium sembarang. -
Jajar Genjang
Jajar genjang adalah bangun datar yang memiliki dua pasang sisi sejajar. Sisi yang sejajar memiliki panjang yang sama. Sudut yang berhadapan pada jajar genjang juga sama besar. Luas jajar genjang dapat dihitung dengan rumus alas dikali tinggi. -
Belah Ketupat
Belah ketupat adalah bangun datar yang memiliki empat sisi sama panjang dan dua diagonal yang saling berpotongan tegak lurus. Diagonal-diagonal tersebut juga saling membagi dua sama panjang. Luas belah ketupat dapat dihitung dengan rumus (d1 × d2) / 2, di mana d1 dan d2 adalah panjang diagonal. -
Layang-Layang
Layang-layang adalah bangun datar yang memiliki dua pasang sisi yang sama panjang dan dua sudut yang berhadapan sama besar. Layang-layang memiliki dua diagonal yang saling berpotongan, tetapi tidak selalu tegak lurus. Luas layang-layang dapat dihitung dengan rumus (d1 × d2) / 2.
Sifat-Sifat Bangun Datar
Setiap jenis bangun datar memiliki sifat-sifat tertentu yang membedakannya dari bangun lainnya. Berikut adalah beberapa sifat umum yang dimiliki oleh berbagai bangun datar:
- Segitiga
- Memiliki tiga sisi dan tiga sudut.
- Jumlah sudut dalam segitiga adalah 180 derajat.
- Segitiga sama sisi memiliki tiga sisi sama panjang dan tiga sudut sama besar.
-
Segitiga siku-siku memiliki satu sudut 90 derajat.
-
Persegi
- Semua sisi sama panjang.
- Semua sudut 90 derajat.
-
Kedua diagonal sama panjang dan saling berpotongan tegak lurus.
-
Persegi Panjang
- Sisi yang berhadapan sama panjang.
- Semua sudut 90 derajat.
-
Kedua diagonal sama panjang, tetapi tidak saling berpotongan tegak lurus.
-
Lingkaran
- Semua titik pada lingkaran memiliki jarak yang sama dari pusat.
- Memiliki diameter dan jari-jari.
-
Tidak memiliki sudut.
-
Trapesium
- Memiliki dua sisi sejajar.
- Dua sisi lainnya tidak sejajar.
-
Jumlah sudut yang berdekatan adalah 180 derajat.
-
Jajar Genjang
- Sisi yang berhadapan sama panjang dan sejajar.
- Sudut yang berhadapan sama besar.
-
Diagonal saling membagi dua sama panjang.
-
Belah Ketupat
- Semua sisi sama panjang.
- Sudut yang berhadapan sama besar.
-
Diagonal saling berpotongan tegak lurus.
-
Layang-Layang
- Dua pasang sisi sama panjang.
- Satu pasang sudut sama besar.
- Diagonal saling berpotongan, tetapi tidak selalu tegak lurus.
Penggunaan Bangun Datar dalam Kehidupan Sehari-Hari
Pemahaman tentang bangun datar tidak hanya berguna dalam studi matematika, tetapi juga dalam berbagai aktivitas sehari-hari. Berikut adalah beberapa contoh penggunaan bangun datar dalam kehidupan nyata:
-
Arsitektur dan Desain Interior
Arsitek dan desainer interior sering menggunakan bangun datar untuk merancang bangunan dan ruangan. Contohnya, bentuk persegi dan persegi panjang sering digunakan dalam pembuatan lantai, dinding, dan furnitur. -
Kerajinan Tangan
Dalam membuat kerajinan tangan seperti origami, kertas lipat, atau lukisan, bangun datar menjadi dasar dari bentuk-bentuk yang ingin diciptakan. -
Olahraga
Lapangan olahraga seperti lapangan sepak bola, bulu tangkis, atau voli memiliki bentuk bangun datar tertentu. Misalnya, lapangan sepak bola memiliki bentuk persegi panjang, sedangkan lapangan bulu tangkis memiliki bentuk persegi panjang yang lebih kecil. -
Teknologi dan Komputer
Dalam dunia komputer dan desain grafis, bangun datar digunakan untuk membuat ikon, logo, dan elemen visual lainnya. -
Pertanian dan Pertamanan
Petani dan tukang kebun sering menggunakan bentuk bangun datar untuk merencanakan lahan pertanian atau taman. Misalnya, taman berbentuk lingkaran atau persegi panjang.
Pentingnya Mempelajari Bangun Datar
Mempelajari bangun datar sangat penting karena memberikan dasar yang kuat dalam memahami konsep geometri. Dengan memahami sifat-sifat dan jenis-jenis bangun datar, kita bisa menghitung luas, keliling, dan volume secara akurat. Selain itu, pemahaman ini juga membantu dalam menyelesaikan masalah matematika yang lebih kompleks, seperti trigonometri dan kalkulus.
Selain itu, mempelajari bangun datar juga meningkatkan kemampuan berpikir logis dan analitis. Kita belajar bagaimana mengidentifikasi bentuk, membandingkan sifat-sifat, dan mencari solusi dari berbagai masalah. Kemampuan ini sangat berguna dalam berbagai bidang pekerjaan, termasuk teknik, seni, dan ilmu pengetahuan.
Lebih jauh lagi, pemahaman tentang bangun datar bisa menjadi dasar untuk mempelajari bangun ruang. Dengan memahami bangun datar, kita bisa lebih mudah memahami cara membentuk bangun tiga dimensi dari bentuk dua dimensi. Hal ini sangat penting dalam bidang seperti desain grafis, arsitektur, dan manufaktur.
Dengan demikian, mempelajari bangun datar bukan hanya sekadar materi pelajaran matematika, tetapi juga keterampilan yang sangat bermanfaat dalam kehidupan sehari-hari. Dengan penguasaan konsep ini, kita bisa lebih mudah memahami dunia sekitar dan mengambil keputusan yang lebih tepat dalam berbagai situasi.