Gerak lurus beraturan (GLB) dan gerak lurus berubah beraturan (GLBB) adalah dua konsep penting dalam ilmu fisika yang sering dipelajari oleh siswa di bangku sekolah. Kedua jenis gerak ini memiliki perbedaan mendasar terkait kecepatan dan percepatan benda yang bergerak. GLB menggambarkan gerakan benda dengan kecepatan tetap, sedangkan GLBB melibatkan perubahan kecepatan secara teratur sepanjang waktu. Dalam kehidupan sehari-hari, kita bisa menemukan contoh dari kedua gerak ini, seperti mobil yang berjalan dengan kecepatan konstan atau kereta api yang mempercepat saat melewati jalur tertentu.
Pemahaman tentang rumus GLB dan GLBB sangat penting untuk menyelesaikan soal-soal fisika yang berkaitan dengan gerak benda. Rumus-rumus ini membantu kita menghitung jarak tempuh, kecepatan akhir, dan waktu yang dibutuhkan benda untuk mencapai suatu titik. Contoh soal dan pembahasan juga menjadi bagian penting dalam memahami penerapan teori tersebut. Artikel ini akan menjelaskan secara lengkap rumus GLB dan GLBB, beserta contoh soal dan penjelasannya agar lebih mudah dipahami oleh para pembaca.
Selain itu, artikel ini juga akan membahas beberapa aplikasi nyata dari GLB dan GLBB dalam kehidupan sehari-hari. Misalnya, GLB dapat ditemukan pada mobil yang bergerak di jalan raya tanpa adanya percepatan, sementara GLBB sering muncul dalam situasi seperti mobil yang mempercepat atau melambat. Pemahaman tentang konsep-konsep dasar ini tidak hanya berguna dalam ujian fisika, tetapi juga dalam analisis gerak benda di berbagai bidang teknik dan rekayasa.
Rumus Gerak Lurus Beraturan (GLB)
Gerak lurus beraturan (GLB) adalah gerak benda yang berlangsung pada lintasan lurus dengan kecepatan yang tetap. Artinya, benda tersebut tidak mengalami percepatan atau perlambatan selama bergerak. Dalam GLB, jarak yang ditempuh benda sama dengan perpindahan benda karena arah geraknya tetap.
Rumus dasar untuk menghitung jarak atau perpindahan dalam GLB adalah:
$$
s = v \times t
$$
Keterangan:
– $ s $ = jarak atau perpindahan (dalam satuan meter)
– $ v $ = kecepatan (dalam satuan meter per detik)
– $ t $ = waktu (dalam satuan detik)
Contoh penerapan GLB dalam kehidupan nyata adalah mobil yang berjalan di jalan raya dengan kecepatan konstan. Jika mobil tersebut bergerak dengan kecepatan 60 km/jam selama 2 jam, maka jarak yang ditempuhnya adalah:
$$
s = 60 \, \text{km/jam} \times 2 \, \text{jam} = 120 \, \text{km}
$$
Dalam GLB, grafik kecepatan terhadap waktu berbentuk garis horizontal, karena kecepatan tetap sepanjang waktu. Sementara itu, grafik perpindahan terhadap waktu berbentuk garis lurus dengan kemiringan yang menunjukkan kecepatan benda.
Rumus Gerak Lurus Berubah Beraturan (GLBB)
Berbeda dengan GLB, GLBB adalah gerak benda yang berlangsung pada lintasan lurus dengan percepatan tetap. Percepatan dalam GLBB dapat positif (mempercepat) atau negatif (melambat). Benda yang bergerak dengan GLBB mengalami perubahan kecepatan secara teratur sepanjang waktu.
Rumus utama dalam GLBB adalah:
$$
v = v_0 + a \times t
$$
Keterangan:
– $ v $ = kecepatan akhir
– $ v_0 $ = kecepatan awal
– $ a $ = percepatan
– $ t $ = waktu
Selain itu, untuk menghitung perpindahan benda dalam GLBB, kita menggunakan rumus:
$$
x = x_0 + v_0 \times t + \frac{1}{2} a \times t^2
$$
Keterangan:
– $ x $ = perpindahan akhir
– $ x_0 $ = perpindahan awal
– $ v_0 $ = kecepatan awal
– $ a $ = percepatan
– $ t $ = waktu
Contoh penerapan GLBB dalam kehidupan nyata adalah mobil yang mempercepat dari kecepatan awal 0 hingga kecepatan 20 m/s dalam waktu 5 detik. Jika percepatannya tetap, maka percepatan mobil tersebut adalah:
$$
a = \frac{v – v_0}{t} = \frac{20 \, \text{m/s} – 0}{5 \, \text{s}} = 4 \, \text{m/s}^2
$$
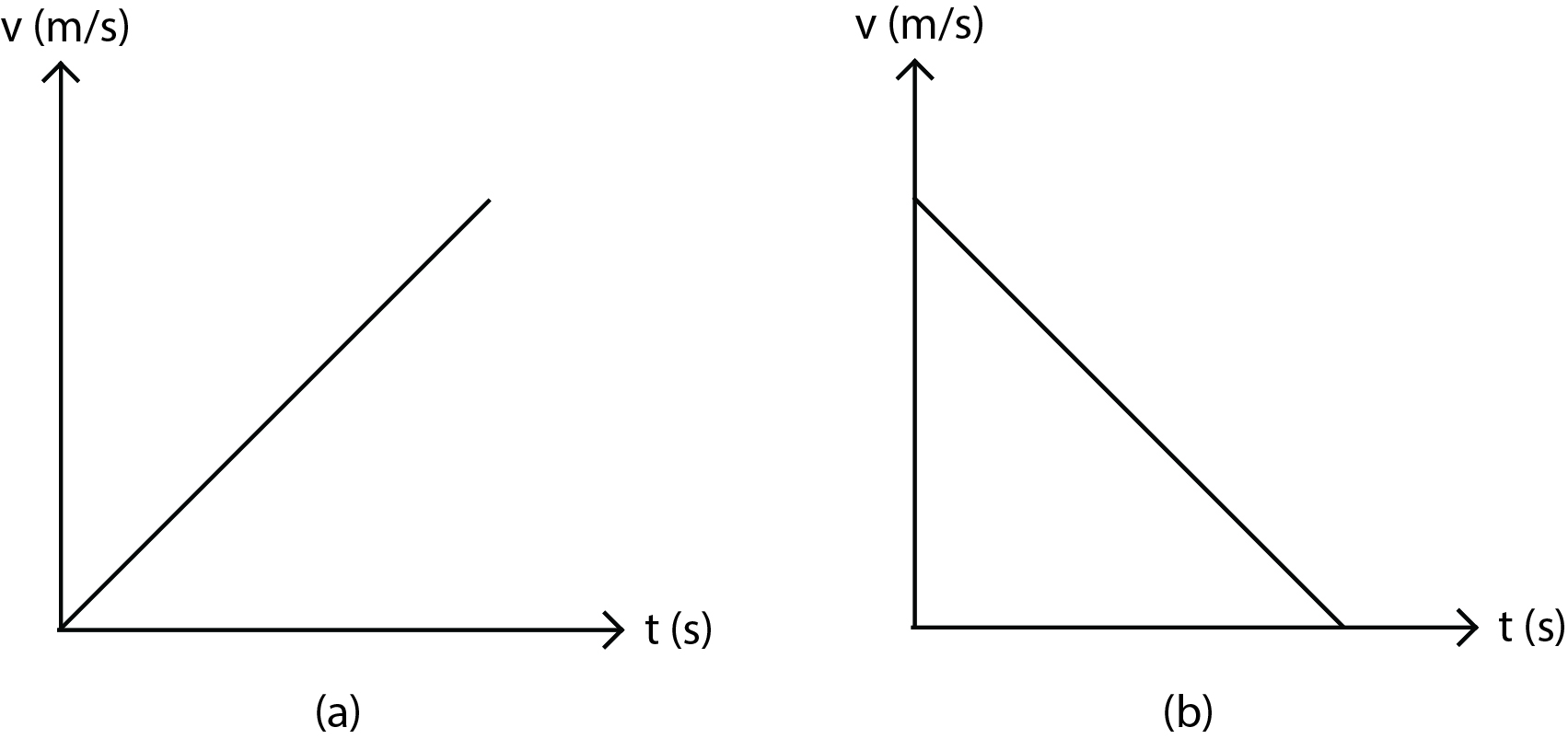
Grafik kecepatan terhadap waktu dalam GLBB berbentuk garis lurus dengan kemiringan yang menunjukkan besar percepatan. Grafik perpindahan terhadap waktu dalam GLBB berbentuk parabola karena perpindahan meningkat secara kuadratik terhadap waktu.
Contoh Soal dan Pembahasan GLB dan GLBB
Contoh Soal 1: Mobil Bergerak dengan GLB
Sebuah mobil bergerak dengan kecepatan tetap 50 km/jam. Hitung jarak yang ditempuh mobil setelah 5 jam!
Pembahasan:
Diketahui:
– $ v = 50 \, \text{km/jam} $
– $ t = 5 \, \text{jam} $
Menggunakan rumus GLB:
$$
s = v \times t = 50 \, \text{km/jam} \times 5 \, \text{jam} = 250 \, \text{km}
$$
Jadi, jarak yang ditempuh mobil adalah 250 km.
Contoh Soal 2: Kereta Api dengan GLB
Kereta api bergerak dengan kecepatan tetap 700 m/s. Hitung jarak yang ditempuh kereta api dalam 0,05 sekon!
Pembahasan:
Diketahui:
– $ v = 700 \, \text{m/s} $
– $ t = 0,05 \, \text{s} $
Menggunakan rumus GLB:
$$
s = v \times t = 700 \, \text{m/s} \times 0,05 \, \text{s} = 35 \, \text{m}
$$
Jadi, jarak yang ditempuh kereta api adalah 35 m.
Contoh Soal 3: Mobil dengan GLBB
Sebuah mobil bergerak dengan kecepatan awal 35 m/s. Setelah 15 sekon, kecepatannya menjadi 50 m/s. Hitung percepatan mobil tersebut!
Pembahasan:
Diketahui:
– $ v_0 = 35 \, \text{m/s} $
– $ v = 50 \, \text{m/s} $
– $ t = 15 \, \text{s} $
Menggunakan rumus GLBB:
$$
a = \frac{v – v_0}{t} = \frac{50 \, \text{m/s} – 35 \, \text{m/s}}{15 \, \text{s}} = \frac{15 \, \text{m/s}}{15 \, \text{s}} = 1 \, \text{m/s}^2
$$
Jadi, percepatan mobil adalah 1 m/s².
Contoh Soal 4: Pesawat Mendarat dengan GLBB
Pesawat mendarat dengan kecepatan 150 m/s dan berhenti dalam waktu 20 sekon. Hitung percepatan dan jarak tempuh pesawat!
Pembahasan:
Diketahui:
– $ v_0 = 150 \, \text{m/s} $
– $ v = 0 \, \text{m/s} $
– $ t = 20 \, \text{s} $
Menghitung percepatan:
$$
a = \frac{v – v_0}{t} = \frac{0 – 150}{20} = -7,5 \, \text{m/s}^2
$$
Menghitung jarak tempuh:
$$
v^2 = v_0^2 + 2a\Delta x \
0 = 150^2 + 2(-7,5)\Delta x \
0 = 22500 – 15\Delta x \
\Delta x = \frac{22500}{15} = 1500 \, \text{m}
$$
Jadi, percepatan pesawat adalah -7,5 m/s² dan jarak tempuhnya adalah 1500 m.
Penerapan GLB dan GLBB dalam Kehidupan Nyata
GLB dan GLBB tidak hanya digunakan dalam soal-soal fisika, tetapi juga dalam berbagai aplikasi nyata. Misalnya, GLB sering digunakan dalam perencanaan lalu lintas dan pengaturan kecepatan kendaraan. Sedangkan GLBB banyak diterapkan dalam bidang teknik, seperti desain mesin, alat transportasi, dan sistem otomatis.
Di bidang olahraga, atlet sering menggunakan prinsip GLB dan GLBB untuk menghitung kecepatan dan jarak yang ditempuh. Contohnya, sprinter yang berlari dengan kecepatan konstan menggunakan GLB, sementara atlet lompat jauh menggunakan GLBB saat melompat dan mengalami percepatan.
Dalam teknologi, GLB dan GLBB juga digunakan dalam pengembangan robot dan kendaraan otonom. Robot yang bergerak di jalur lurus dengan kecepatan tetap menggunakan prinsip GLB, sedangkan kendaraan otonom yang mempercepat atau melambat menggunakan prinsip GLBB.
Kesimpulan
GLB dan GLBB adalah dua konsep dasar dalam fisika yang menggambarkan gerak benda pada lintasan lurus. GLB memiliki kecepatan tetap, sedangkan GLBB memiliki percepatan tetap. Rumus-rumus yang digunakan dalam keduanya sangat penting untuk menyelesaikan berbagai soal dan masalah nyata. Pemahaman tentang GLB dan GLBB tidak hanya berguna dalam ujian, tetapi juga dalam berbagai bidang kehidupan sehari-hari. Dengan memahami prinsip-prinsip ini, kita dapat lebih mudah menginterpretasikan gerak benda dan menerapkannya dalam kehidupan sehari-hari.