Lingkaran adalah salah satu bentuk geometri yang paling umum ditemukan dalam kehidupan sehari-hari. Dari roda kendaraan hingga benda-benda seperti cincin, uang koin, dan bahkan bentuk alam seperti matahari, lingkaran memiliki peran penting dalam berbagai aspek kehidupan. Namun, di balik penampilannya yang sederhana, lingkaran mengandung banyak unsur-unsur penting yang perlu dipahami untuk memahami sifat-sifatnya secara lebih mendalam. Dengan memahami unsur-unsur ini, kita bisa lebih mudah menghitung luas, keliling, dan berbagai ukuran lain yang terkait dengan lingkaran. Artikel ini akan membahas pengertian lingkaran serta berbagai unsur-unsur yang ada di dalamnya, lengkap dengan penjelasan dan contoh nyata.
Lingkaran merupakan bangun datar dua dimensi yang dibentuk oleh kumpulan titik-titik yang memiliki jarak sama terhadap suatu titik pusat. Titik-titik tersebut membentuk sebuah lengkungan tertutup yang disebut keliling lingkaran. Setiap lingkaran pasti memiliki luas dan keliling, yang dapat dihitung menggunakan rumus matematika khusus. Salah satu hal yang sering digunakan dalam perhitungan lingkaran adalah nilai π (phi), yang nilainya sekitar 3,14 atau 22/7. Nilai ini sangat penting dalam menentukan hasil perhitungan luas dan keliling lingkaran. Dengan pemahaman dasar tentang lingkaran, kita bisa lebih mudah memahami konsep-konsep lanjutan seperti diameter, jari-jari, tembereng, dan lainnya.
Unsur-unsur lingkaran tidak hanya sekadar bagian dari bentuk geometris, tetapi juga memiliki fungsi masing-masing dalam berbagai perhitungan dan aplikasi nyata. Misalnya, jari-jari dan diameter digunakan untuk menentukan ukuran lingkaran, sedangkan busur dan tembereng digunakan dalam perhitungan luas daerah tertentu. Selain itu, sudut pusat dan sudut keliling juga memiliki peran penting dalam memahami hubungan antara garis-garis dalam lingkaran. Dengan memahami semua unsur ini, kita bisa lebih mudah mengaplikasikan konsep lingkaran dalam berbagai situasi, baik dalam matematika maupun dalam kehidupan sehari-hari.
Pengertian Lingkaran
Lingkaran adalah bentuk geometri dua dimensi yang terbentuk dari himpunan titik-titik yang memiliki jarak yang sama terhadap satu titik pusat. Jarak tersebut disebut sebagai jari-jari, dan titik pusat menjadi pusat simetri dari lingkaran. Karena semua titik pada lingkaran memiliki jarak yang sama terhadap titik pusat, lingkaran memiliki bentuk yang sempurna dan tidak memiliki sudut atau sisi tajam. Hal ini membuat lingkaran menjadi bentuk yang sangat efisien dalam berbagai aplikasi, seperti roda kendaraan yang dirancang agar dapat bergerak lancar tanpa hambatan.
Dalam matematika, lingkaran sering digunakan untuk menjelaskan berbagai konsep seperti luas, keliling, dan sudut. Rumus-rumus yang digunakan dalam perhitungan lingkaran sangat bergantung pada nilai π (phi), yang merupakan rasio antara keliling lingkaran dan diameternya. Nilai π biasanya dinyatakan sebagai 3,14 atau 22/7, tergantung pada kebutuhan perhitungan. Dengan memahami konsep dasar lingkaran, kita bisa lebih mudah menghitung berbagai parameter yang terkait dengan lingkaran, seperti luas, keliling, dan sudut-sudut dalam lingkaran.
Selain itu, lingkaran juga memiliki sifat-sifat unik yang membuatnya berbeda dari bentuk-bentuk geometri lainnya. Misalnya, lingkaran memiliki simetri putar tak terbatas karena setiap titik pada lingkaran memiliki jarak yang sama terhadap titik pusat. Sifat ini membuat lingkaran sangat cocok digunakan dalam berbagai bidang, termasuk teknik, seni, dan ilmu pengetahuan. Dengan demikian, memahami pengertian lingkaran adalah langkah awal yang penting untuk menguasai konsep-konsep lanjutan dalam geometri.
Unsur-Unsur Utama dalam Lingkaran
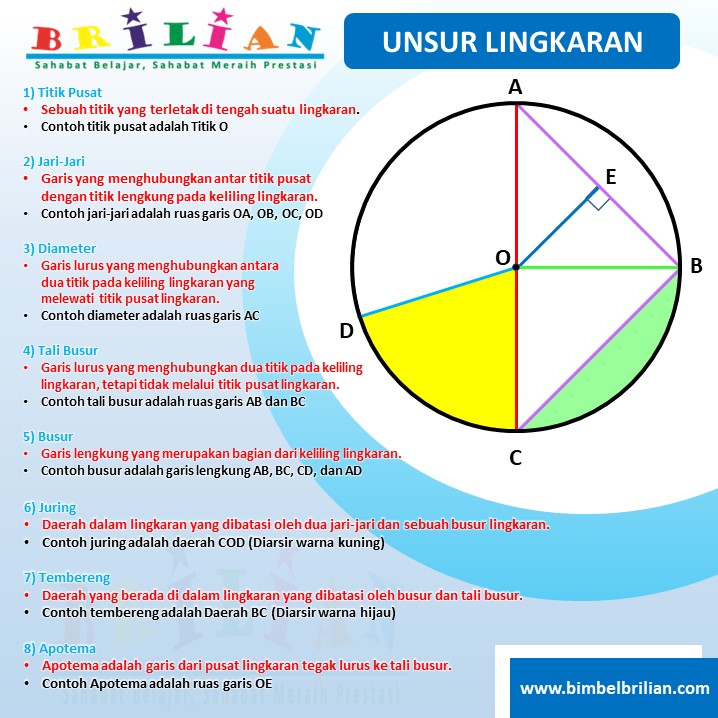
Sebuah lingkaran terdiri dari beberapa unsur utama yang masing-masing memiliki peran penting dalam perhitungan dan analisis. Unsur-unsur ini meliputi jari-jari, diameter, titik pusat, busur, tali busur, tembereng, apotema, juring, sudut keliling, dan sudut pusat. Masing-masing dari unsur ini memiliki definisi dan fungsi tersendiri yang harus dipahami untuk menguasai konsep lingkaran secara menyeluruh.
Jari-jari adalah garis lurus yang menghubungkan titik pusat lingkaran dengan titik pada kelilingnya. Diameter, di sisi lain, adalah garis lurus yang menghubungkan dua titik pada keliling lingkaran dan melewati titik pusat. Dengan demikian, diameter memiliki panjang dua kali jari-jari. Titik pusat adalah titik tengah dari lingkaran yang menjadi acuan utama dalam pembentukan lingkaran. Busur adalah bagian dari keliling lingkaran yang dibentuk oleh dua titik pada lingkaran. Tali busur adalah garis lurus yang menghubungkan dua titik pada keliling lingkaran tanpa melewati titik pusat.
Tembereng adalah daerah yang dibatasi oleh busur dan tali busur, sedangkan apotema adalah jarak terpendek dari tali busur ke titik pusat lingkaran. Juring adalah daerah yang dibatasi oleh dua jari-jari dan satu busur. Sudut keliling adalah sudut yang dibentuk oleh dua tali busur yang bertemu di satu titik pada keliling lingkaran, sedangkan sudut pusat adalah sudut yang dibentuk oleh dua jari-jari yang bertemu di titik pusat lingkaran. Dengan memahami semua unsur ini, kita bisa lebih mudah menghitung berbagai parameter lingkaran dan memahami hubungan antar unsur-unsur tersebut.
Fungsi dan Aplikasi Unsur-unsur Lingkaran
Setiap unsur dalam lingkaran memiliki fungsi dan aplikasi yang berbeda dalam berbagai bidang. Misalnya, jari-jari dan diameter digunakan untuk menentukan ukuran lingkaran, baik dalam perhitungan luas maupun keliling. Dalam kehidupan sehari-hari, jari-jari dan diameter sering digunakan dalam desain roda kendaraan, kunci, atau benda-benda lain yang berbentuk lingkaran. Dengan memahami hubungan antara jari-jari dan diameter, kita bisa lebih mudah menghitung ukuran lingkaran sesuai kebutuhan.
Busur dan tali busur juga memiliki peran penting dalam berbagai aplikasi, terutama dalam perhitungan luas daerah tertentu. Contohnya, dalam arsitektur, busur digunakan untuk membuat bentuk lengkung pada jembatan atau pintu. Tembereng dan juring sering digunakan dalam perhitungan luas area yang dibatasi oleh busur dan tali busur. Apotema, di sisi lain, digunakan dalam perhitungan jarak terdekat dari tali busur ke titik pusat, yang sangat berguna dalam desain struktur yang stabil.
Sudut keliling dan sudut pusat memiliki peran penting dalam geometri, terutama dalam memahami hubungan antara garis-garis dalam lingkaran. Dalam studi matematika, kedua jenis sudut ini sering digunakan dalam pembuktian teorema dan perhitungan sudut dalam lingkaran. Dengan memahami fungsi dan aplikasi masing-masing unsur, kita bisa lebih mudah mengaplikasikan konsep lingkaran dalam berbagai situasi nyata.
Perhitungan Luas dan Keliling Lingkaran
Perhitungan luas dan keliling lingkaran adalah salah satu aspek penting dalam memahami konsep lingkaran. Rumus luas lingkaran adalah π × r², di mana r adalah jari-jari lingkaran. Sedangkan rumus keliling lingkaran adalah 2 × π × r atau π × d, dengan d adalah diameter lingkaran. Nilai π (phi) biasanya diambil sebagai 3,14 atau 22/7, tergantung pada kebutuhan perhitungan. Dengan menggunakan rumus-rumus ini, kita bisa dengan mudah menghitung luas dan keliling lingkaran sesuai dengan data yang diberikan.
Pemahaman tentang luas dan keliling lingkaran sangat penting dalam berbagai bidang, termasuk teknik, desain grafis, dan ilmu pengetahuan. Misalnya, dalam konstruksi bangunan, perhitungan luas lingkaran digunakan untuk menentukan ukuran permukaan yang berbentuk lingkaran, seperti kolam renang atau taman lingkaran. Dalam desain grafis, luas dan keliling lingkaran digunakan untuk menciptakan bentuk-bentuk visual yang menarik dan proporsional.
Selain itu, perhitungan luas dan keliling lingkaran juga digunakan dalam berbagai masalah matematika, seperti menentukan ukuran lingkaran yang dibutuhkan untuk menutupi suatu area tertentu atau menghitung jumlah bahan yang diperlukan untuk membuat benda berbentuk lingkaran. Dengan memahami rumus dan cara menggunakannya, kita bisa lebih mudah menghadapi berbagai tantangan yang melibatkan lingkaran dalam kehidupan sehari-hari.
Studi Kasus: Aplikasi Lingkaran dalam Teknologi Modern
Dalam teknologi modern, lingkaran memiliki peran yang sangat penting dalam berbagai bidang, termasuk komputer, otomotif, dan teknologi informasi. Contohnya, dalam industri otomotif, roda kendaraan dirancang dengan bentuk lingkaran untuk memastikan gerakan yang mulus dan efisien. Desain roda berbentuk lingkaran memungkinkan gesekan yang rendah dan distribusi beban yang merata, sehingga meningkatkan kenyamanan dan keamanan berkendara. Dalam teknologi komputer, lingkaran digunakan dalam desain layar monitor, mouse, dan berbagai komponen lainnya yang memerlukan bentuk yang simetris dan presisi tinggi.
Selain itu, dalam teknologi informasi, lingkaran digunakan dalam desain antarmuka pengguna (UI) dan algoritma grafis. Bentuk lingkaran sering digunakan dalam ikon, tombol, dan elemen visual lainnya karena sifatnya yang estetis dan mudah diidentifikasi. Dalam sistem navigasi, seperti GPS, lingkaran digunakan untuk menentukan radius jangkauan atau area yang dicakup oleh sinyal. Dengan memahami konsep lingkaran, kita bisa lebih mudah memahami bagaimana teknologi modern mengintegrasikan bentuk-bentuk geometris untuk menciptakan solusi yang efektif dan efisien.
Studi kasus ini menunjukkan bahwa lingkaran bukan hanya sekadar bentuk geometris, tetapi juga memiliki peran vital dalam berbagai aspek kehidupan. Dengan memahami konsep lingkaran dan aplikasinya, kita bisa lebih mudah mengapresiasi keindahan dan fungsionalitas bentuk-bentuk geometris dalam dunia nyata.