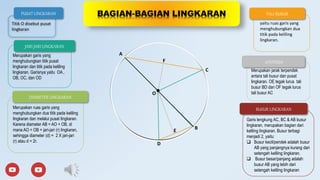
Lingkaran adalah salah satu bentuk geometri yang paling sederhana namun memiliki banyak kegunaan dalam matematika. Lingkaran terdiri dari berbagai bagian yang masing-masing memiliki fungsi khusus dalam perhitungan dan analisis. Memahami bagian-bagian lingkaran sangat penting untuk mempelajari konsep-konsep seperti keliling, luas, sudut, dan hubungan antara titik-titik di dalam atau di sekitar lingkaran. Dalam artikel ini, kita akan membahas secara detail mengenai bagian-bagian lingkaran dan fungsinya dalam matematika, termasuk radius, diameter, busur, tali busur, juring, tembereng, dan pusat lingkaran. Penjelasan ini dirancang agar mudah dipahami oleh siswa maupun siapa pun yang tertarik dengan matematika dasar.
Lingkaran didefinisikan sebagai himpunan semua titik yang memiliki jarak sama dari suatu titik tertentu yang disebut pusat lingkaran. Jarak tersebut disebut radius. Radius menjadi dasar dari semua pengukuran dalam lingkaran karena ukuran radius menentukan besar kecilnya lingkaran. Diameter adalah garis lurus yang melewati pusat lingkaran dan menghubungkan dua titik pada lingkaran. Diameter memiliki panjang dua kali radius, sehingga dapat dihitung dengan rumus diameter = 2 × radius. Kedua bagian ini sangat penting dalam menghitung keliling dan luas lingkaran.
Selain radius dan diameter, ada juga bagian lain seperti busur, tali busur, juring, dan tembereng. Busur adalah bagian dari keliling lingkaran yang terletak antara dua titik. Tali busur adalah garis lurus yang menghubungkan dua titik pada lingkaran, sedangkan juring adalah area yang dibatasi oleh dua radius dan sebuah busur. Tembereng adalah area yang dibatasi oleh tali busur dan busur. Semua bagian ini digunakan dalam berbagai aplikasi matematika, mulai dari perhitungan luas daerah hingga pemecahan masalah dalam trigonometri. Memahami fungsi masing-masing bagian ini akan membantu dalam memperdalam pemahaman tentang lingkaran.
Pusat Lingkaran
Pusat lingkaran adalah titik yang berada di tengah-tengah lingkaran dan merupakan titik acuan untuk mengukur jarak ke semua titik pada lingkaran. Titik ini sangat penting karena semua bagian lingkaran, seperti radius dan diameter, diukur dari pusat. Tanpa pusat, tidak mungkin menentukan ukuran atau bentuk lingkaran. Pusat juga menjadi titik awal dalam membuat diagram lingkaran atau dalam menggambar lingkaran menggunakan alat seperti jangka. Dalam persamaan matematika, pusat lingkaran biasanya dilambangkan dengan (h, k) dalam bentuk umum persamaan lingkaran, yaitu (x – h)² + (y – k)² = r², di mana r adalah radius.
Radius
Radius adalah jarak dari pusat lingkaran ke tepi lingkaran. Radius menjadi parameter utama dalam menentukan ukuran lingkaran. Panjang radius memengaruhi keliling dan luas lingkaran. Misalnya, jika radius meningkat, maka keliling dan luas lingkaran juga akan meningkat. Dalam perhitungan matematika, radius sering digunakan untuk menghitung luas lingkaran dengan rumus L = πr² dan keliling lingkaran dengan rumus K = 2πr. Radius juga digunakan dalam berbagai bidang ilmu seperti fisika, teknik, dan desain grafis. Contohnya, dalam desain grafis, radius digunakan untuk membuat lingkaran sempurna atau bentuk-bentuk melengkung.
Diameter
Diameter adalah garis lurus yang melewati pusat lingkaran dan menghubungkan dua titik pada lingkaran. Diameter memiliki panjang dua kali radius, sehingga bisa dihitung dengan rumus D = 2r. Diameter sering digunakan dalam perhitungan matematika, terutama ketika ingin mengetahui ukuran lingkaran secara keseluruhan. Misalnya, dalam menghitung keliling lingkaran, diameter bisa digunakan dalam rumus K = πD. Selain itu, diameter juga digunakan dalam berbagai aplikasi praktis, seperti dalam pembuatan roda kendaraan, di mana ukuran diameter menentukan ukuran roda. Dalam studi geometri, diameter sering digunakan untuk menentukan hubungan antara lingkaran dan objek lain, seperti segitiga atau persegi.
Busur
Busur adalah bagian dari keliling lingkaran yang terletak antara dua titik. Busur bisa berupa busur kecil atau busur besar, tergantung pada panjangnya. Panjang busur dapat dihitung dengan menggunakan rumus L = θr, di mana θ adalah sudut pusat dalam radian dan r adalah radius. Busur digunakan dalam berbagai perhitungan, seperti dalam trigonometri dan geometri. Misalnya, dalam trigonometri, busur digunakan untuk menghitung nilai sinus, kosinus, dan tangen. Dalam seni dan desain, busur sering digunakan untuk membuat bentuk-bentuk melengkung yang indah.
Tali Busur
Tali busur adalah garis lurus yang menghubungkan dua titik pada lingkaran. Tali busur berbeda dengan diameter karena tidak selalu melewati pusat lingkaran. Panjang tali busur dapat dihitung dengan menggunakan rumus L = 2r sin(θ/2), di mana θ adalah sudut pusat dalam derajat. Tali busur digunakan dalam berbagai perhitungan, seperti dalam menghitung luas segmen lingkaran. Dalam studi geometri, tali busur sering digunakan untuk menentukan hubungan antara lingkaran dan segitiga. Contohnya, dalam segitiga yang terbentuk dari tiga titik pada lingkaran, tali busur bisa digunakan untuk menghitung sudut-sudut segitiga tersebut.
Juring
Juring adalah area yang dibatasi oleh dua radius dan sebuah busur. Juring mirip dengan potongan pizza yang terbentuk dari dua garis lurus dan satu lengkungan. Luas juring dapat dihitung dengan rumus L = (θ/360) × πr², di mana θ adalah sudut pusat dalam derajat dan r adalah radius. Juring digunakan dalam berbagai perhitungan, seperti dalam menghitung luas daerah tertentu dalam lingkaran. Dalam studi trigonometri, juring sering digunakan untuk menghitung nilai-nilai fungsi trigonometri. Dalam kehidupan sehari-hari, juring bisa ditemukan dalam bentuk potongan kue atau pizza.
Tembereng
Tembereng adalah area yang dibatasi oleh tali busur dan busur. Tembereng mirip dengan juring, tetapi hanya dibatasi oleh satu busur dan satu tali busur. Luas tembereng dapat dihitung dengan mengurangi luas juring dengan luas segitiga yang dibentuk oleh dua radius dan tali busur. Rumus luas tembereng adalah L = (L_juring – L_segitiga). Tembereng digunakan dalam berbagai perhitungan, seperti dalam menghitung luas daerah tertentu dalam lingkaran. Dalam studi geometri, tembereng sering digunakan untuk menentukan hubungan antara lingkaran dan segitiga. Contohnya, dalam segitiga yang terbentuk dari tiga titik pada lingkaran, tembereng bisa digunakan untuk menghitung luas segitiga tersebut.
Penggunaan Bagian-Bagian Lingkaran dalam Matematika
Bagian-bagian lingkaran memiliki berbagai fungsi dalam matematika, baik dalam teori maupun aplikasi. Dalam teori matematika, bagian-bagian ini digunakan untuk menghitung keliling, luas, dan sudut dalam lingkaran. Dalam aplikasi nyata, bagian-bagian ini digunakan dalam berbagai bidang seperti teknik, astronomi, dan desain grafis. Misalnya, dalam teknik, radius dan diameter digunakan untuk menghitung ukuran roda atau pipa. Dalam astronomi, busur dan sudut digunakan untuk menghitung posisi bintang dan planet. Dalam desain grafis, tali busur dan juring digunakan untuk menciptakan bentuk-bentuk melengkung yang indah. Dengan memahami bagian-bagian lingkaran, kita dapat lebih mudah memahami konsep-konsep matematika yang lebih kompleks.